Bulls and Cows + Solver
Table of Contents
Bulls and Cows
- This code cracking logic game similar to Mastermind
- The computer picks a random 4 digit number
- The player makes a guess as to what that 4 digit number is
- Each guess is scored by the number of "bulls" and "cows"
- A "bull" means that a digit is in the right position
- A "cow" means that the digit is in the string but not in the right position
- The score doesn't tell you which digit is a "bull" or "cow" only how many digits are each
- For example if the secret is
1234and the player guesses4130the score would be1B2C, the3being the "bull" and the4and1being in the code but not in the correct position - Another requirement of the secret code is that it has no repeating digits
- Wikipedia: Bulls and Cows
- I was inspired to work on this while reading Land of Lisp, by Conrad Barski, and the popular game Wordle.
Project Scope
- This is a series of functions that allow you to play the game bulls and cows inside a common lisp REPL
- You will be able to play the number guessing game or invoke the solver to watch the computer guess the answer
Implementation
Setting up the game
- This code defines the game setup function and global variable
*secret-code* - The setup function,
bulls-cows-setup, will generate a list of 4 random integers and store that in*secret-code* - There secret code will not have the digit zero in it
- The algorithm for generating a random code without repeats is as follows:
- Start with a list of all wanted digits and the length of the secret
- Check the length of the secret, if
0returnnil - Pick a random index out of the wanted digits
- Return the cons of the digit using the random index and a recursive call to the generate code function
- In the recursive call, slice the randomly picked index from the wanted digits list
- Additionally reduce the length by 1 in the recursive call
- The setup function returns
tto not spoil the secret code
(defparameter *secret-code* nil) (defparameter *code-length* 4) (defparameter *code-digits* '(1 2 3 4 5 6 7 8 9)) (defparameter *code-min* 1234) (defparameter *code-max* 9876) (defun generate-secret (digits len) (unless (<= len 0) (let* ((index (random (length digits))) (digit (nth index digits))) (cons digit (generate-secret (concatenate 'list (subseq digits 0 index) (subseq digits (1+ index))) (- len 1)))))) (defun bulls-cows-setup () (setf *secret-code* (generate-secret *code-digits* *code-length*)) t)
Scoring a guess
- The player of the game can make a guess on the secret code with the
guessfunction - An example call of the
guesswould look like this(guess 4130)- In order to convert a number
4130to the list(4 1 3 0)we can convert to string then into a list - To convert string numeric characters into numbers again we can use
digit-char-p - We will leave a method that accepts the code as a list as well, this will be good for solvers
- In order to convert a number
- The return will be the score of the guess measured in bulls and cows
- If the secret code is
1234and you guess(guess 4130)the score should be1B2C
(defun guess-code (code) (when (= (length code) *code-length*) (let ((bulls 0) (cows 0) (i 0)) (loop (if (= (nth i code) (nth i *secret-code*)) (setf bulls (1+ bulls)) (when (member (nth i code) *secret-code*) (setf cows (1+ cows)))) (when (= (1+ i) *code-length*) (return)) (setf i (1+ i))) `(,bulls B ,cows C)))) (defun guess (num) (let ((code (map 'list #'digit-char-p (write-to-string num)))) (guess-code code)))
Evaluating scores
- A human player is able to interpret the output of the
guessfunction to know if they have won the game or not - A computer will need a function to easily know if the correct guess has been encountered
- The
equalfunction can compare the symbol values with the winning score(4 B 0 C)
(defun win-p (score) (equal score `(,*code-length* B 0 C)))
Solvers
- Each of these solvers use the output of the
guessfunction to try to automate finding the secret code - Each solver will count how many times it calls
guessand return that number along with the secret code - There are 3024 different possible secret codes (nPr where n = 9 digits and r = 4 length code)
Random Guesses
- One of the simplest solvers to implement is to continue to check random guesses to see if they are correct
- This will not be using the clues at all to inform the next guess
- Because of this it is a very inconsistent solution for finding the right answer
- This will use the
generate-secretmethod for randomly picking a guess - While simple to implement this solver it is random how long it will take
- Additionally, it might not find the answer at all
(defparameter *max-guesses* 100000) (defun run-random-solver () (let ((count 0) (code (generate-secret *code-digits* *code-length*)) (solution-found nil)) (loop (cond ((>= count *max-guesses*) (return)) ((win-p (guess-code code)) (setf solution-found t) (return)) (t (setf count (1+ count)) (setf code (generate-secret *code-digits* *code-length*))))) (when solution-found (list code count)))))
Brute Force
- This solver will enumerate through all the possible codes and see if it is the right one
- It will not attempt to read the score to understand how close a guess might be
- It is definitely not an efficient method for checking for the code
- It does have the benefit of not being random and always taking the same amount of time to find the answer
- Additionally it should always find an answer
- Next Permutation
- In order to achieve this we need a function to calculate the next permutation from a given one
- The first permutation should be
1234the last permutation should be9876 - The key to this algorithm is a predicate that verifies if a number is a valid permutation
- If that predicate fails just increment the number and try again
- This removes one instance of the value being checked and then ensures that there is not another instance of it in the list
(defun valid-code-p (num) (let* ((code (map 'list #'digit-char-p (write-to-string num))) (no-repeats (every #'identity (mapcar #'(lambda (m) (not (member m (remove-if #'(lambda (n) (= n m)) code :count 1)))) code))) (no-illegal-chars (every #'(lambda (n) (member n *code-digits*)) code))) (and no-repeats no-illegal-chars)))
- This function finds the next lexical code from a given input
- It continuously increments the number until a valid code is found
(defun next-code (num) (cond ((valid-code-p (1+ num)) (1+ num)) (t (next-code (1+ num)))))
- Solver
(defun run-brute-force-solver () (let ((code *code-min*) (count 0)) (loop (cond ((win-p (guess code)) (return)) ((= code *code-max*) (return)) (t (setf code (next-code code)) (setf count (1+ count))))) (list code count)))
Cows Score Solver
- This solver will use the score to determine if a digit is part of the code or not
- It won't use the bulls portion of the score
- The first step is to look for a set of
*code-length*digits that have a score of 0 bulls and 0 cows- In order to do this we iterate through consecutive sets in the list
- If non of them have a 0 score then we will shuffle the list and try again
- Once the digits we are sure are not part of the solution are found we remove them from our local copy of the digit list
- We repeat the above process until length of local digits divided by the
*code-length*is less than 2- In the case of this game we only need to find one set of zero score digits for that to be true
- With the digit list now less that 2 *
*code-length*we repeat the process but looking for a score totaling to*code-length* - Once we find that we shuffle that score randomly until it causes
win-pto return true
- Sub List
- In order to rule out digits we need a way to get a consecutive sublist of digits
- This function will get a consecutive list of count number items from a list
- If the start index + count is greater than the length of the list it will wrap around to the beginning
(defun sublist (start count list) (let ((i 1) (s (list (nth start list)))) (loop (when (>= i count) (return)) (push (nth (mod (+ start i) (length list)) list) (cdr (last s))) (setf i (1+ i))) s))
- Shuffle List
- In order to shuffle a list we rotate it
ntimes, wherenis the length of the list - Each shuffle will randomly select two digits and swap them
(defun shuffle-list (list) (let ((i 0)) (loop (when (>= i (length list)) (return)) (rotatef (nth (random (length list)) list) (nth (random (length list)) list)) (setf i (1+ i))) list))
- In order to shuffle a list we rotate it
- Score Total
- This function sums the numerical portion of the bulls and cows score
- For example
(1 B 2 C)would total to 3 - This is useful for determining if none of the digits tested are in the solution
(defun score-total (score) (+ (car score) (caddr score)))
- Find sublist with score total
- This function will use consecutive sublists looking for a set that has a given score total
- It will generate a sublist starting at each index in the list
- If no item is found it will shuffle the list and try again
- This function tracks how many times it calls
guess-code - Once the set is found it returns a list of both the set and the guess count
(defun find-set-with-score (search-set wanted-score) (let* ((list (copy-list search-set)) (count 1) (g (sublist 0 *code-length* list)) (score (score-total (guess-code g)))) (loop (when (= score wanted-score) (return)) (let ((i 0)) (loop (when (= score wanted-score) (return)) (setf i (1+ i)) (when (>= i (length list)) (return)) (setf g (sublist i *code-length* list)) (setf count (1+ count)) (setf score (score-total (guess-code g))))) (shuffle-list list)) (list g count)))
- Solver
(defun run-cows-solver () (let ((digits (copy-list *code-digits*)) (count 0) (not-code-set nil) (code-set nil) (results nil) (score nil)) (setf results (find-set-with-score digits 0)) (setf not-code-set (car results)) (setf count (+ count (cadr results))) (remove-if #'(lambda (n) (member n not-code-set)) digits) (setf results (find-set-with-score digits *code-length*)) (setf code-set (car results)) (setf count (+ count (cadr results))) (loop (setf score (guess-code code-set)) (setf count (1+ count)) (when (win-p score) (return)) (shuffle-list code-set)) (list code-set count)))
Solver Data
- This code runs each solver 10 times and generates a table with the results
(defun get-solver-data () (let ((count 1) (results nil)) (loop (when (> count 10) (return)) (bulls-cows-setup) (let ((result (list count (cadr (run-random-solver)) (cadr (run-brute-force-solver)) (cadr (run-cows-solver))))) (if (null results) (setf results (list result)) (push result (cdr (last results))))) (setf count (1+ count))) results)) (get-solver-data)
| run | random | brute force | cow |
|---|---|---|---|
| 1 | 1113 | 2487 | 201 |
| 2 | 3563 | 1261 | 133 |
| 3 | 67 | 2463 | 120 |
| 4 | 1999 | 2571 | 193 |
| 5 | 319 | 915 | 369 |
| 6 | 6237 | 1341 | 190 |
| 7 | 4079 | 2463 | 153 |
| 8 | 2299 | 578 | 78 |
| 9 | 3055 | 587 | 281 |
| 10 | 488 | 278 | 35 |
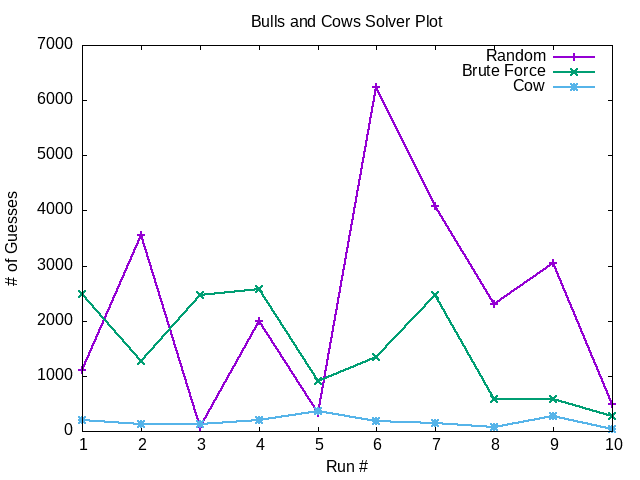
- Looking at the graph the cow solver performed the best
- Using the score value to inform the guesses significantly reduced the amount of guesses needed
- random performed the worst by far
- brute force never exceeds the total number of permutations (3024) which makes sense